Poker Math & Probabilities (Texas Hold'em) The following tables provide various probabilities and odds for many of the common events in a game of Texas hold 'em. Odds% Example Win% 330-to-1 0.30% JJ v 77 80% v 20% 220-to-1 0.45% 55 v AQ 55% v 45% 110-to-1 0.90% 55 v AQs 50% v 50%. Wizard Of Odds Poker Probabilities We always list the most important terms & Wizard Of Odds Poker Probabilities conditions that you need to know about. With that being said, there are several Wizard Of Odds Poker Probabilities well known and trusted casinos that offer a first deposit bonus of 400% up to €40.
On This Page
Introduction
Rules
The craps games allowed the Vegas standard 3-4-5X odds for a combined house edge between the pass and odds of 0.37% and 0.27% between the don't and laying odds. The field paid 3 to 1 on a 12. Hop bets paid 15 to 1 and 30 to 1. Wizard Of Odds Blackjack House Edge Calculator, casino santa fe torneo poker, anti gambling ad singapore germany, second chance poker strategy.
- A single 52-card deck is used. All cards count as its poker value. Aces may be high or low.
- One player is designated as the dealer, usually with a laminated marker. This person does not have to physically deal the game. However it is important that a symbolic dealer position rotate around the table.
- The player to the dealer's left must make a 'small blind' bet. The player to the left of the small blind must make a 'big blind' bet. The amounts of both blinds should be specified in advance. The purpose of the blinds is to get the ball rolling with some money in the pot.
- Two cards shall be dealt down to each player, starting with the person to the dealer's left.
- The player to the left of the big blind must either call or raise the big blind bet. The play in turn will go around the table according to normal poker rules, which I assume the reader already knows. Table rules will specify any limits on the size or number of allowed raises.
- The small blind may also raise the big blind. If nobody raises the big blind the player making the big blind has the option to raise his own bet. The term for this is the 'big blind option.'
- Three community cards will be dealt face up in the center of the table. This is called the 'flop.'
- Another round of betting will ensue, starting with the player to the dealer's left.
- A fourth community card will be dealt face up in the center of the table. This card is called the 'turn.'
- Another round of betting will ensue, starting with the player to the dealer's left. Generally the minimum bet is double the first two rounds of betting.
- A fifth and final community card will be dealt face up in the center of the table. This card is called the 'river.'
- Another round of betting will ensue, starting with the player to the dealer's left. The minimum bet is generally the same as the previous round.
Each player still in the game at the end will determine the highest poker value among his own two cards and the five community cards. It is NOT a requirement that the player use both of his own cards. The player with the hand of highest poker value shall win. Following are the hand rankings.
- Straight flush: Five consecutive and suited cards. For example 5, 6, 7, 8, 9.
- Four of a kind: Four cards of the same rank, plus any fifth card. For example Q, Q, Q, Q ,4.
- Full house: Three of a kind and a pair. For example 6, 6, 6, J , J.
- Flush: Any five cards of the same suit, except for a higher ranking straight flush. For example A, Q, 8, 4 , 3.
- Straight: Five consecutive cards, except for a higher ranking straight flush. For example 8, 9, 10, J, Q.
- Three of a kind: Three cards of the same rank, plus any other two cards. For example 5, 5, 5, Q ,2 .
- Two pair: Two pairs, plus any fifth card. For example 8, 8, 2, 2 ,Q .
- Pair: A pair and any other three cards. For example 7, 7, 2, 5 ,A .
- ? High: Any five cards that do not form any higher poker hand. A king high hand for example might be K, Q, 7, 5 ,4 .
- If two or more players have poker values of the same rank then the individual cards will be used to break the tie. If necessary all five cards will be considered.
- I get asked a lot whether the two unused cards in a player's hand are used to break a tie. The answer is a firm NO. The two unused cards do not matter.
- If a new player arrives at the table he should either wait for the big blind position or put up an amount equal to the big blind, amounting to a call of the big blind.
- If a bet is made after another player runs out of money, then a separate pot is created. The player that ran out of money is not eligible to win the second pot. If more than one player runs out of money then multiple separate pots can be created.
- In formal games players may not bet with cash or buy chips with cash in the middle of a hand.
- There are numerous rules of etiquette, which I won't get into.
- There house may set the betting rules. There are three main types. A 'structured' game features raises of specified amounts. For example a '3/6 game' would mean that raises after the deal and flop are $3, and after the turn and river are $6. There is usually a limit to the number of raises a player may make, typically three. A 'pot limit' game has structured minimum raises but the maximum raise may be anything up to the amount in the pot at the time the raise is made. A 'no limit' game also has structured minimum raises but there is no maximum raise.
Examples
Example 1
Board: A, 2, 4, 5, 6
Player 1: J, 6
Player 2: 7, Q
Player 1 wins. Both have an ace high flush, so the second highest card is considered. Player 1's jack beats player 2's 7. The only way to have a flush tie is if the flush is entirely on the board and no hole cards are higher than the lowest card on the board in the same suit.
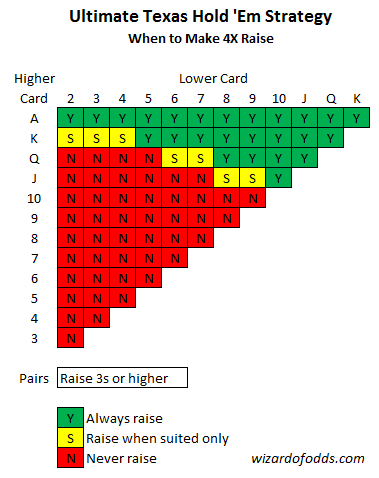
Example 2
Board: J, A, 7, 5, 6
Player 1: 2, J
Player 2: 10, J
Player 2 wins. Both have a pair of jacks so the singletons are considered. High highet singleton in both hands is an ace so the second highest singleton is considered. Player 1's second highest singleton is a 7, compared to player 2's 10. A 10 beats a 7 so player 2 wins.
Example 3

Board: A, A, K, Q, J
Player 1: Q, J
Player 2: Q, 2
Tie. Both have a two pair of aces and queens, with a king singleton. Some people incorrectly believe that in such cases the unused cards are considered, in this case player 1's pair of jacks beating player 2's jack/2. Only the top five cards matter. The jacks and deuce are irrelevant.
One of the most important aspects of Texas Hold'em is the value of each two-card hand before the flop. The decision of how to play your first two cards is something you face every hand, and the value of your first two cards is highly correlated to your probability of winning.
The following table shows my power rating for each initial 2-card hand in a 10-player game. The numbers are on a 0 to 40 scale. Basically, you should only play hands that are dark green, blue, or purple. Of course you should be more be more liberal in late position and picky in early position. If forced I would say you should need 10 points in late position and 19 points in early position to call the big blind. If your table is loose, as if often the case online, you can play a bit looser yourself.
Use the top table if you have a pair, the middle table if your cards are suited, and the bottom table if your cards are unsuited. Except for a pair,look up your high card along the left and your low card along the top.
Following are the links to my tables of the value of each intial hand according to the number of players. The 10-player section explains the methodology for creating the table table.
Pot Odds
The following table shows the probability of making various hands after the flop and the correct 'pot odds.' The pot odds are the breakeven ratio of money in the pot to the amount you have to bet for the player to be indifferent about calling, assuming the player would definitely win if he makes the hand (a big if) and there are no additional bets (another big if). This table is a good starting point the player should make mental adjustments for the probability of winning without making the hand, losing with making the hand, and expected future bets. The odds of a two pair improving to a full house are the same as those for four to an inside straight.
Pot Odds — After Flop
| Hand | Probability of Making Hand | Pot Odds |
|---|---|---|
| Four to a flush | 34.97% | 1.86 |
| Four to an outside straight | 31.45% | 2.18 |
| Four to an inside straight | 16.47% | 5.07 |
The next table shows the pot odds after the turn.
Pot Odds — After Turn
| Hand | Probability of Making Hand | Pot Odds |
|---|---|---|
| 4 to a flush | 19.57% | 4.11 |
| 4 to an outside straight | 17.39% | 4.75 |
| 4 to an inside straight | 8.70% | 10.50 |
Hand Strength Calculator
I'm proud to present my new and improved Poker Odds Calculator. Enter any situation in Texas Hold 'Em, and it will tell you the probability of each possible outcome.
Poker Tournament Calculator
My Poker Tournament Calculator will determine each player's probability, for up to nine players, of finishing in each place, and his expected share of any prize pool, assuming equal skill among all players. It produces the same results as what is known as the Independent Chip Model.
Internal Links
- Pinapple — Strategy and analysis of which card to discard before the flop.
- Bad Beat Jackpots: What is the Probability of Hitting one?
- Texas Hold 'Em Dominated Hand Probabilities: What is the probability one of your opponents has similar, and better, hole cards than yours?
Written by:Michael Shackleford

The mathematics of gambling are a collection of probability applications encountered in games of chance and can be included in game theory. From a mathematical point of view, the games of chance are experiments generating various types of aleatory events, the probability of which can be calculated by using the properties of probability on a finite space of events.
Experiments, events, probability spaces[edit]
The technical processes of a game stand for experiments that generate aleatory events. Here are a few examples:
- Throwing the dice in craps is an experiment that generates events such as occurrences of certain numbers on the dice, obtaining a certain sum of the shown numbers, and obtaining numbers with certain properties (less than a specific number, higher than a specific number, even, uneven, and so on). The sample space of such an experiment is {1, 2, 3, 4, 5, 6} for rolling one die or {(1, 1), (1, 2), ..., (1, 6), (2, 1), (2, 2), ..., (2, 6), ..., (6, 1), (6, 2), ..., (6, 6)} for rolling two dice. The latter is a set of ordered pairs and counts 6 x 6 = 36 elements. The events can be identified with sets, namely parts of the sample space. For example, the event occurrence of an even number is represented by the following set in the experiment of rolling one die: {2, 4, 6}.
- Spinning the roulette wheel is an experiment whose generated events could be the occurrence of a certain number, of a certain color or a certain property of the numbers (low, high, even, uneven, from a certain row or column, and so on). The sample space of the experiment involving spinning the roulette wheel is the set of numbers the roulette holds: {1, 2, 3, ..., 36, 0, 00} for the American roulette, or {1, 2, 3, ..., 36, 0} for the European. The event occurrence of a red number is represented by the set {1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36}. These are the numbers inscribed in red on the roulette wheel and table.
- Dealing cards in blackjack is an experiment that generates events such as the occurrence of a certain card or value as the first card dealt, obtaining a certain total of points from the first two cards dealt, exceeding 21 points from the first three cards dealt, and so on. In card games we encounter many types of experiments and categories of events. Each type of experiment has its own sample space. For example, the experiment of dealing the first card to the first player has as its sample space the set of all 52 cards (or 104, if played with two decks). The experiment of dealing the second card to the first player has as its sample space the set of all 52 cards (or 104), less the first card dealt. The experiment of dealing the first two cards to the first player has as its sample space a set of ordered pairs, namely all the 2-size arrangements of cards from the 52 (or 104). In a game with one player, the event the player is dealt a card of 10 points as the first dealt card is represented by the set of cards {10♠, 10♣, 10♥, 10♦, J♠, J♣, J♥, J♦, Q♠, Q♣, Q♥, Q♦, K♠, K♣, K♥, K♦}. The event the player is dealt a total of five points from the first two dealt cards is represented by the set of 2-size combinations of card values {(A, 4), (2, 3)}, which in fact counts 4 x 4 + 4 x 4 = 32 combinations of cards (as value and symbol).
- In 6/49 lottery, the experiment of drawing six numbers from the 49 generates events such as drawing six specific numbers, drawing five numbers from six specific numbers, drawing four numbers from six specific numbers, drawing at least one number from a certain group of numbers, etc. The sample space here is the set of all 6-size combinations of numbers from the 49.
- In draw poker, the experiment of dealing the initial five card hands generates events such as dealing at least one certain card to a specific player, dealing a pair to at least two players, dealing four identical symbols to at least one player, and so on. The sample space in this case is the set of all 5-card combinations from the 52 (or the deck used).
- Dealing two cards to a player who has discarded two cards is another experiment whose sample space is now the set of all 2-card combinations from the 52, less the cards seen by the observer who solves the probability problem. For example, if you are in play in the above situation and want to figure out some odds regarding your hand, the sample space you should consider is the set of all 2-card combinations from the 52, less the three cards you hold and less the two cards you discarded. This sample space counts the 2-size combinations from 47.
The probability model[edit]
A probability model starts from an experiment and a mathematical structure attached to that experiment, namely the space (field) of events. The event is the main unit probability theory works on. In gambling, there are many categories of events, all of which can be textually predefined. In the previous examples of gambling experiments we saw some of the events that experiments generate. They are a minute part of all possible events, which in fact is theset of all parts of the sample space.
For a specific game, the various types of events can be:
- Events related to your own play or to opponents' play;
- Events related to one person's play or to several persons' play;
- Immediate events or long-shot events.
Each category can be further divided into several other subcategories, depending on the game referred to. These events can be literally defined, but it must be done very carefully when framing a probability problem. From a mathematical point of view, the events are nothing more than subsets and the space of events is a Boolean algebra. Among these events, we find elementary and compound events, exclusive and nonexclusive events, and independent and non-independent events.
In the experiment of rolling a die:
- Event {3, 5} (whose literal definition is occurrence of 3 or 5) is compound because {3, 5}= {3} U {5};
- Events {1}, {2}, {3}, {4}, {5}, {6} are elementary;
- Events {3, 5} and {4} are incompatible orexclusive because their intersection is empty; that is, they cannot occur simultaneously;
- Events {1, 2, 5} and {2, 5} are nonexclusive, because their intersection is not empty;
- In the experiment of rolling two dice one after another, the events obtaining 3 on the first die and obtaining 5 on the second die are independent because the occurrence of the second event is not influenced by the occurrence of the first, and vice versa.
In the experiment of dealing the pocket cards in Texas Hold'em Poker:
- The event of dealing (3♣, 3♦) to a player is an elementary event;
- The event of dealing two 3's to a player is compound because is the union of events (3♣, 3♠), (3♣, 3♥), (3♣, 3♦), (3♠, 3♥), (3♠, 3♦) and (3♥, 3♦);
- The events player 1 is dealt a pair of kings and player 2 is dealt a pair of kings are nonexclusive (they can both occur);
- The events player 1 is dealt two connectors of hearts higher than J and player 2 is dealt two connectors of hearts higher than J are exclusive (only one can occur);
- The events player 1 is dealt (7, K) and player 2 is dealt (4, Q) are non-independent (the occurrence of the second depends on the occurrence of the first, while the same deck is in use).
These are a few examples of gambling events, whose properties of compoundness, exclusiveness and independency are easily observable. Theseproperties are very important in practical probability calculus.
The complete mathematical model is given by the probability field attached to the experiment, which is the triple sample space—field of events—probability function. For any game of chance, the probability model is of the simplest type—the sample space is finite, the space of events is the set of parts of the sample space, implicitly finite, too, and the probability function is given by the definition of probability on a finite space of events:
Combinations[edit]
Games of chance are also good examples of combinations, permutations and arrangements, which are met at every step: combinations of cards in a player's hand, on the table or expected in any card game; combinations of numbers when rolling several dice once; combinations of numbers in lottery and bingo; combinations of symbols in slots; permutations and arrangements in a race to be bet on, and the like. Combinatorial calculus is an important part of gambling probability applications. In games of chance, most of the gambling probability calculus in which we use the classical definition of probability reverts to counting combinations. The gaming events can be identified with sets, which often are sets of combinations. Thus, we can identify an event with a combination.
For example, in a five draw poker game, the event at least one player holds a four of a kind formation can be identified with the set of all combinations of (xxxxy) type, where x and y are distinct values of cards. This set has 13C(4,4)(52-4)=624 combinations. Possible combinations are (3♠ 3♣ 3♥ 3♦ J♣) or (7♠ 7♣ 7♥ 7♦ 2♣). These can be identified with elementary events that the event to be measured consists of.
Expectation and strategy[edit]
Games of chance are not merely pure applications of probability calculus and gaming situations are not just isolated events whose numerical probability is well established through mathematical methods; they are also games whose progress is influenced by human action. In gambling, the human element has a striking character. The player is not only interested in the mathematical probability of the various gaming events, but he or she has expectations from the games while a major interaction exists. To obtain favorable results from this interaction, gamblers take into account all possible information, including statistics, to build gaming strategies. The oldest and most common betting system is the martingale, or doubling-up, system on even-money bets, in which bets are doubled progressively after each loss until a win occurs. This system probably dates back to the invention of the roulette wheel. Two other well-known systems, also based on even-money bets, are the d'Alembert system (based on theorems of the French mathematician Jean Le Rond d'Alembert), in which the player increases his bets by one unit after each loss but decreases it by one unit after each win, and the Labouchere system (devised by the British politician Henry Du Pré Labouchere, although the basis for it was invented by the 18th-century French philosopher Marie-Jean-Antoine-Nicolas de Caritat, marquis de Condorcet), in which the player increases or decreases his bets according to a certain combination of numbers chosen in advance.[1][2] The predicted average gain or loss is called expectation or expected value and is the sum of the probability of each possible outcome of the experiment multiplied by its payoff (value). Thus, it represents the average amount one expects to win per bet if bets with identical odds are repeated many times. A game or situation in which the expected value for the player is zero (no net gain nor loss) is called a fair game. The attribute fair refers not to the technical process of the game, but to the chance balance house (bank)–player.
Even though the randomness inherent in games of chance would seem to ensure their fairness (at least with respect to the players around a table—shuffling a deck or spinning a wheel do not favor any player except if they are fraudulent), gamblers always search and wait for irregularities in this randomness that will allow them to win. It has been mathematically proved that, in ideal conditions of randomness, and with negative expectation, no long-run regular winning is possible for players of games of chance. Most gamblers accept this premise, but still work on strategies to make them win either in the short term or over the long run.

House advantage or edge[edit]
Casino games provide a predictable long-term advantage to the casino, or 'house' while offering the player the possibility of a large short-term payout. Some casino games have a skill element, where the player makes decisions; such games are called 'random with a tactical element.' While it is possible through skillful play to minimize the house advantage, it is extremely rare that a player has sufficient skill to completely eliminate his inherent long-term disadvantage (the house edge or house vigorish) in a casino game. The common belief is that such a skill set would involve years of training, extraordinary memory, and numeracy, and/or acute visual or even aural observation, as in the case of wheel clocking in Roulette. For more examples see Advantage gambling.
The player's disadvantage is a result of the casino not paying winning wagers according to the game's 'true odds', which are the payouts that would be expected considering the odds of a wager either winning or losing. For example, if a game is played by wagering on the number that would result from the roll of one die, true odds would be 5 times the amount wagered since there is a 1/6 probability of any single number appearing. However, the casino may only pay 4 times the amount wagered for a winning wager.
The house edge (HE) or vigorish is defined as the casino profit expressed as a percentage of the player's original bet. In games such as Blackjack or Spanish 21, the final bet may be several times the original bet, if the player doubles or splits.
Example: In American Roulette, there are two zeroes and 36 non-zero numbers (18 red and 18 black). If a player bets $1 on red, his chance of winning $1 is therefore 18/38 and his chance of losing $1 (or winning -$1) is 20/38.
The player's expected value, EV = (18/38 x 1) + (20/38 x -1) = 18/38 - 20/38 = -2/38 = -5.26%. Therefore, the house edge is 5.26%. After 10 rounds, play $1 per round, the average house profit will be 10 x $1 x 5.26% = $0.53.Of course, it is not possible for the casino to win exactly 53 cents; this figure is the average casino profit from each player if it had millions of players each betting 10 rounds at $1 per round.
The house edge of casino games varies greatly with the game. Keno can have house edges up to 25% and slot machines can have up to 15%, while most Australian Pontoon games have house edges between 0.3% and 0.4%.
The calculation of the Roulette house edge was a trivial exercise; for other games, this is not usually the case. Combinatorial analysis and/or computer simulation is necessary to complete the task.
In games that have a skill element, such as Blackjack or Spanish 21, the house edge is defined as the house advantage from optimal play (without the use of advanced techniques such as card counting or shuffle tracking), on the first hand of the shoe (the container that holds the cards). The set of the optimal plays for all possible hands is known as 'basic strategy' and is highly dependent on the specific rules, and even the number of decks used. Good Blackjack and Spanish 21 games have to house edges below 0.5%.
Online slot games often have a published Return to Player (RTP) percentage that determines the theoretical house edge. Some software developers choose to publish the RTP of their slot games while others do not.[3] Despite the set-theoretical RTP, almost any outcome is possible in the short term.[4] RTP is the percentage of the jackpot or prize money that can be regurgitated from the slot machine. Say the dealer does a 20% set, then there is a potential for jackpot 1: 5 to come out, but the fact is of course not this big considering the patterns or symbols that exist in online slot games are so diverse. [5]
Standard deviation[edit]
The luck factor in a casino game is quantified using standard deviation (SD). The standard deviation of a simple game like Roulette can be simply calculated because of the binomial distribution of successes (assuming a result of 1 unit for a win, and 0 units for a loss). For the binomial distribution, SD is equal to npq{displaystyle {sqrt {npq}}}, where n{displaystyle n} is the number of rounds played, p{displaystyle p} is the probability of winning, and q{displaystyle q} is the probability of losing. Furthermore, if we flat bet at 10 units per round instead of 1 unit, the range of possible outcomes increases 10 fold. Therefore, SD for Roulette even-money bet is equal to 2bnpq{displaystyle 2b{sqrt {npq}}}, where b{displaystyle b} is the flat bet per round, n{displaystyle n} is the number of rounds, p=18/38{displaystyle p=18/38}, and q=20/38{displaystyle q=20/38}.
After enough large number of rounds the theoretical distribution of the total win converges to the normal distribution, giving a good possibility to forecast the possible win or loss. For example, after 100 rounds at $1 per round, the standard deviation of the win (equally of the loss) will be 2⋅$1⋅100⋅18/38⋅20/38≈$9.99{displaystyle 2cdot $1cdot {sqrt {100cdot 18/38cdot 20/38}}approx $9.99}. After 100 rounds, the expected loss will be 100⋅$1⋅2/38≈$5.26{displaystyle 100cdot $1cdot 2/38approx $5.26}.

Example 2
Board: J, A, 7, 5, 6
Player 1: 2, J
Player 2: 10, J
Player 2 wins. Both have a pair of jacks so the singletons are considered. High highet singleton in both hands is an ace so the second highest singleton is considered. Player 1's second highest singleton is a 7, compared to player 2's 10. A 10 beats a 7 so player 2 wins.
Example 3
Board: A, A, K, Q, J
Player 1: Q, J
Player 2: Q, 2
Tie. Both have a two pair of aces and queens, with a king singleton. Some people incorrectly believe that in such cases the unused cards are considered, in this case player 1's pair of jacks beating player 2's jack/2. Only the top five cards matter. The jacks and deuce are irrelevant.
One of the most important aspects of Texas Hold'em is the value of each two-card hand before the flop. The decision of how to play your first two cards is something you face every hand, and the value of your first two cards is highly correlated to your probability of winning.
The following table shows my power rating for each initial 2-card hand in a 10-player game. The numbers are on a 0 to 40 scale. Basically, you should only play hands that are dark green, blue, or purple. Of course you should be more be more liberal in late position and picky in early position. If forced I would say you should need 10 points in late position and 19 points in early position to call the big blind. If your table is loose, as if often the case online, you can play a bit looser yourself.
Use the top table if you have a pair, the middle table if your cards are suited, and the bottom table if your cards are unsuited. Except for a pair,look up your high card along the left and your low card along the top.
Following are the links to my tables of the value of each intial hand according to the number of players. The 10-player section explains the methodology for creating the table table.
Pot Odds
The following table shows the probability of making various hands after the flop and the correct 'pot odds.' The pot odds are the breakeven ratio of money in the pot to the amount you have to bet for the player to be indifferent about calling, assuming the player would definitely win if he makes the hand (a big if) and there are no additional bets (another big if). This table is a good starting point the player should make mental adjustments for the probability of winning without making the hand, losing with making the hand, and expected future bets. The odds of a two pair improving to a full house are the same as those for four to an inside straight.
Pot Odds — After Flop
| Hand | Probability of Making Hand | Pot Odds |
|---|---|---|
| Four to a flush | 34.97% | 1.86 |
| Four to an outside straight | 31.45% | 2.18 |
| Four to an inside straight | 16.47% | 5.07 |
The next table shows the pot odds after the turn.
Pot Odds — After Turn
| Hand | Probability of Making Hand | Pot Odds |
|---|---|---|
| 4 to a flush | 19.57% | 4.11 |
| 4 to an outside straight | 17.39% | 4.75 |
| 4 to an inside straight | 8.70% | 10.50 |
Hand Strength Calculator
I'm proud to present my new and improved Poker Odds Calculator. Enter any situation in Texas Hold 'Em, and it will tell you the probability of each possible outcome.
Poker Tournament Calculator
My Poker Tournament Calculator will determine each player's probability, for up to nine players, of finishing in each place, and his expected share of any prize pool, assuming equal skill among all players. It produces the same results as what is known as the Independent Chip Model.
Internal Links
- Pinapple — Strategy and analysis of which card to discard before the flop.
- Bad Beat Jackpots: What is the Probability of Hitting one?
- Texas Hold 'Em Dominated Hand Probabilities: What is the probability one of your opponents has similar, and better, hole cards than yours?
Written by:Michael Shackleford
The mathematics of gambling are a collection of probability applications encountered in games of chance and can be included in game theory. From a mathematical point of view, the games of chance are experiments generating various types of aleatory events, the probability of which can be calculated by using the properties of probability on a finite space of events.
Experiments, events, probability spaces[edit]
The technical processes of a game stand for experiments that generate aleatory events. Here are a few examples:
- Throwing the dice in craps is an experiment that generates events such as occurrences of certain numbers on the dice, obtaining a certain sum of the shown numbers, and obtaining numbers with certain properties (less than a specific number, higher than a specific number, even, uneven, and so on). The sample space of such an experiment is {1, 2, 3, 4, 5, 6} for rolling one die or {(1, 1), (1, 2), ..., (1, 6), (2, 1), (2, 2), ..., (2, 6), ..., (6, 1), (6, 2), ..., (6, 6)} for rolling two dice. The latter is a set of ordered pairs and counts 6 x 6 = 36 elements. The events can be identified with sets, namely parts of the sample space. For example, the event occurrence of an even number is represented by the following set in the experiment of rolling one die: {2, 4, 6}.
- Spinning the roulette wheel is an experiment whose generated events could be the occurrence of a certain number, of a certain color or a certain property of the numbers (low, high, even, uneven, from a certain row or column, and so on). The sample space of the experiment involving spinning the roulette wheel is the set of numbers the roulette holds: {1, 2, 3, ..., 36, 0, 00} for the American roulette, or {1, 2, 3, ..., 36, 0} for the European. The event occurrence of a red number is represented by the set {1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36}. These are the numbers inscribed in red on the roulette wheel and table.
- Dealing cards in blackjack is an experiment that generates events such as the occurrence of a certain card or value as the first card dealt, obtaining a certain total of points from the first two cards dealt, exceeding 21 points from the first three cards dealt, and so on. In card games we encounter many types of experiments and categories of events. Each type of experiment has its own sample space. For example, the experiment of dealing the first card to the first player has as its sample space the set of all 52 cards (or 104, if played with two decks). The experiment of dealing the second card to the first player has as its sample space the set of all 52 cards (or 104), less the first card dealt. The experiment of dealing the first two cards to the first player has as its sample space a set of ordered pairs, namely all the 2-size arrangements of cards from the 52 (or 104). In a game with one player, the event the player is dealt a card of 10 points as the first dealt card is represented by the set of cards {10♠, 10♣, 10♥, 10♦, J♠, J♣, J♥, J♦, Q♠, Q♣, Q♥, Q♦, K♠, K♣, K♥, K♦}. The event the player is dealt a total of five points from the first two dealt cards is represented by the set of 2-size combinations of card values {(A, 4), (2, 3)}, which in fact counts 4 x 4 + 4 x 4 = 32 combinations of cards (as value and symbol).
- In 6/49 lottery, the experiment of drawing six numbers from the 49 generates events such as drawing six specific numbers, drawing five numbers from six specific numbers, drawing four numbers from six specific numbers, drawing at least one number from a certain group of numbers, etc. The sample space here is the set of all 6-size combinations of numbers from the 49.
- In draw poker, the experiment of dealing the initial five card hands generates events such as dealing at least one certain card to a specific player, dealing a pair to at least two players, dealing four identical symbols to at least one player, and so on. The sample space in this case is the set of all 5-card combinations from the 52 (or the deck used).
- Dealing two cards to a player who has discarded two cards is another experiment whose sample space is now the set of all 2-card combinations from the 52, less the cards seen by the observer who solves the probability problem. For example, if you are in play in the above situation and want to figure out some odds regarding your hand, the sample space you should consider is the set of all 2-card combinations from the 52, less the three cards you hold and less the two cards you discarded. This sample space counts the 2-size combinations from 47.
The probability model[edit]
A probability model starts from an experiment and a mathematical structure attached to that experiment, namely the space (field) of events. The event is the main unit probability theory works on. In gambling, there are many categories of events, all of which can be textually predefined. In the previous examples of gambling experiments we saw some of the events that experiments generate. They are a minute part of all possible events, which in fact is theset of all parts of the sample space.
For a specific game, the various types of events can be:
- Events related to your own play or to opponents' play;
- Events related to one person's play or to several persons' play;
- Immediate events or long-shot events.
Each category can be further divided into several other subcategories, depending on the game referred to. These events can be literally defined, but it must be done very carefully when framing a probability problem. From a mathematical point of view, the events are nothing more than subsets and the space of events is a Boolean algebra. Among these events, we find elementary and compound events, exclusive and nonexclusive events, and independent and non-independent events.
In the experiment of rolling a die:
- Event {3, 5} (whose literal definition is occurrence of 3 or 5) is compound because {3, 5}= {3} U {5};
- Events {1}, {2}, {3}, {4}, {5}, {6} are elementary;
- Events {3, 5} and {4} are incompatible orexclusive because their intersection is empty; that is, they cannot occur simultaneously;
- Events {1, 2, 5} and {2, 5} are nonexclusive, because their intersection is not empty;
- In the experiment of rolling two dice one after another, the events obtaining 3 on the first die and obtaining 5 on the second die are independent because the occurrence of the second event is not influenced by the occurrence of the first, and vice versa.
In the experiment of dealing the pocket cards in Texas Hold'em Poker:
- The event of dealing (3♣, 3♦) to a player is an elementary event;
- The event of dealing two 3's to a player is compound because is the union of events (3♣, 3♠), (3♣, 3♥), (3♣, 3♦), (3♠, 3♥), (3♠, 3♦) and (3♥, 3♦);
- The events player 1 is dealt a pair of kings and player 2 is dealt a pair of kings are nonexclusive (they can both occur);
- The events player 1 is dealt two connectors of hearts higher than J and player 2 is dealt two connectors of hearts higher than J are exclusive (only one can occur);
- The events player 1 is dealt (7, K) and player 2 is dealt (4, Q) are non-independent (the occurrence of the second depends on the occurrence of the first, while the same deck is in use).
These are a few examples of gambling events, whose properties of compoundness, exclusiveness and independency are easily observable. Theseproperties are very important in practical probability calculus.
The complete mathematical model is given by the probability field attached to the experiment, which is the triple sample space—field of events—probability function. For any game of chance, the probability model is of the simplest type—the sample space is finite, the space of events is the set of parts of the sample space, implicitly finite, too, and the probability function is given by the definition of probability on a finite space of events:
Combinations[edit]
Games of chance are also good examples of combinations, permutations and arrangements, which are met at every step: combinations of cards in a player's hand, on the table or expected in any card game; combinations of numbers when rolling several dice once; combinations of numbers in lottery and bingo; combinations of symbols in slots; permutations and arrangements in a race to be bet on, and the like. Combinatorial calculus is an important part of gambling probability applications. In games of chance, most of the gambling probability calculus in which we use the classical definition of probability reverts to counting combinations. The gaming events can be identified with sets, which often are sets of combinations. Thus, we can identify an event with a combination.
For example, in a five draw poker game, the event at least one player holds a four of a kind formation can be identified with the set of all combinations of (xxxxy) type, where x and y are distinct values of cards. This set has 13C(4,4)(52-4)=624 combinations. Possible combinations are (3♠ 3♣ 3♥ 3♦ J♣) or (7♠ 7♣ 7♥ 7♦ 2♣). These can be identified with elementary events that the event to be measured consists of.
Expectation and strategy[edit]
Games of chance are not merely pure applications of probability calculus and gaming situations are not just isolated events whose numerical probability is well established through mathematical methods; they are also games whose progress is influenced by human action. In gambling, the human element has a striking character. The player is not only interested in the mathematical probability of the various gaming events, but he or she has expectations from the games while a major interaction exists. To obtain favorable results from this interaction, gamblers take into account all possible information, including statistics, to build gaming strategies. The oldest and most common betting system is the martingale, or doubling-up, system on even-money bets, in which bets are doubled progressively after each loss until a win occurs. This system probably dates back to the invention of the roulette wheel. Two other well-known systems, also based on even-money bets, are the d'Alembert system (based on theorems of the French mathematician Jean Le Rond d'Alembert), in which the player increases his bets by one unit after each loss but decreases it by one unit after each win, and the Labouchere system (devised by the British politician Henry Du Pré Labouchere, although the basis for it was invented by the 18th-century French philosopher Marie-Jean-Antoine-Nicolas de Caritat, marquis de Condorcet), in which the player increases or decreases his bets according to a certain combination of numbers chosen in advance.[1][2] The predicted average gain or loss is called expectation or expected value and is the sum of the probability of each possible outcome of the experiment multiplied by its payoff (value). Thus, it represents the average amount one expects to win per bet if bets with identical odds are repeated many times. A game or situation in which the expected value for the player is zero (no net gain nor loss) is called a fair game. The attribute fair refers not to the technical process of the game, but to the chance balance house (bank)–player.
Even though the randomness inherent in games of chance would seem to ensure their fairness (at least with respect to the players around a table—shuffling a deck or spinning a wheel do not favor any player except if they are fraudulent), gamblers always search and wait for irregularities in this randomness that will allow them to win. It has been mathematically proved that, in ideal conditions of randomness, and with negative expectation, no long-run regular winning is possible for players of games of chance. Most gamblers accept this premise, but still work on strategies to make them win either in the short term or over the long run.
House advantage or edge[edit]
Casino games provide a predictable long-term advantage to the casino, or 'house' while offering the player the possibility of a large short-term payout. Some casino games have a skill element, where the player makes decisions; such games are called 'random with a tactical element.' While it is possible through skillful play to minimize the house advantage, it is extremely rare that a player has sufficient skill to completely eliminate his inherent long-term disadvantage (the house edge or house vigorish) in a casino game. The common belief is that such a skill set would involve years of training, extraordinary memory, and numeracy, and/or acute visual or even aural observation, as in the case of wheel clocking in Roulette. For more examples see Advantage gambling.
The player's disadvantage is a result of the casino not paying winning wagers according to the game's 'true odds', which are the payouts that would be expected considering the odds of a wager either winning or losing. For example, if a game is played by wagering on the number that would result from the roll of one die, true odds would be 5 times the amount wagered since there is a 1/6 probability of any single number appearing. However, the casino may only pay 4 times the amount wagered for a winning wager.
The house edge (HE) or vigorish is defined as the casino profit expressed as a percentage of the player's original bet. In games such as Blackjack or Spanish 21, the final bet may be several times the original bet, if the player doubles or splits.
Example: In American Roulette, there are two zeroes and 36 non-zero numbers (18 red and 18 black). If a player bets $1 on red, his chance of winning $1 is therefore 18/38 and his chance of losing $1 (or winning -$1) is 20/38.
The player's expected value, EV = (18/38 x 1) + (20/38 x -1) = 18/38 - 20/38 = -2/38 = -5.26%. Therefore, the house edge is 5.26%. After 10 rounds, play $1 per round, the average house profit will be 10 x $1 x 5.26% = $0.53.Of course, it is not possible for the casino to win exactly 53 cents; this figure is the average casino profit from each player if it had millions of players each betting 10 rounds at $1 per round.
The house edge of casino games varies greatly with the game. Keno can have house edges up to 25% and slot machines can have up to 15%, while most Australian Pontoon games have house edges between 0.3% and 0.4%.
The calculation of the Roulette house edge was a trivial exercise; for other games, this is not usually the case. Combinatorial analysis and/or computer simulation is necessary to complete the task.
In games that have a skill element, such as Blackjack or Spanish 21, the house edge is defined as the house advantage from optimal play (without the use of advanced techniques such as card counting or shuffle tracking), on the first hand of the shoe (the container that holds the cards). The set of the optimal plays for all possible hands is known as 'basic strategy' and is highly dependent on the specific rules, and even the number of decks used. Good Blackjack and Spanish 21 games have to house edges below 0.5%.
Online slot games often have a published Return to Player (RTP) percentage that determines the theoretical house edge. Some software developers choose to publish the RTP of their slot games while others do not.[3] Despite the set-theoretical RTP, almost any outcome is possible in the short term.[4] RTP is the percentage of the jackpot or prize money that can be regurgitated from the slot machine. Say the dealer does a 20% set, then there is a potential for jackpot 1: 5 to come out, but the fact is of course not this big considering the patterns or symbols that exist in online slot games are so diverse. [5]
Standard deviation[edit]
The luck factor in a casino game is quantified using standard deviation (SD). The standard deviation of a simple game like Roulette can be simply calculated because of the binomial distribution of successes (assuming a result of 1 unit for a win, and 0 units for a loss). For the binomial distribution, SD is equal to npq{displaystyle {sqrt {npq}}}, where n{displaystyle n} is the number of rounds played, p{displaystyle p} is the probability of winning, and q{displaystyle q} is the probability of losing. Furthermore, if we flat bet at 10 units per round instead of 1 unit, the range of possible outcomes increases 10 fold. Therefore, SD for Roulette even-money bet is equal to 2bnpq{displaystyle 2b{sqrt {npq}}}, where b{displaystyle b} is the flat bet per round, n{displaystyle n} is the number of rounds, p=18/38{displaystyle p=18/38}, and q=20/38{displaystyle q=20/38}.
After enough large number of rounds the theoretical distribution of the total win converges to the normal distribution, giving a good possibility to forecast the possible win or loss. For example, after 100 rounds at $1 per round, the standard deviation of the win (equally of the loss) will be 2⋅$1⋅100⋅18/38⋅20/38≈$9.99{displaystyle 2cdot $1cdot {sqrt {100cdot 18/38cdot 20/38}}approx $9.99}. After 100 rounds, the expected loss will be 100⋅$1⋅2/38≈$5.26{displaystyle 100cdot $1cdot 2/38approx $5.26}.
The 3 sigma range is six times the standard deviation: three above the mean, and three below. Therefore, after 100 rounds betting $1 per round, the result will very probably be somewhere between −$5.26−3⋅$9.99{displaystyle -$5.26-3cdot $9.99} and −$5.26+3⋅$9.99{displaystyle -$5.26+3cdot $9.99}, i.e., between -$34 and $24. There is still a ca. 1 to 400 chance that the result will be not in this range, i.e. either the win will exceed $24, or the loss will exceed $34.
The standard deviation for the even-money Roulette bet is one of the lowest out of all casinos games. Most games, particularly slots, have extremely high standard deviations. As the size of the potential payouts increase, so does the standard deviation.
Unfortunately, the above considerations for small numbers of rounds are incorrect, because the distribution is far from normal. Moreover, the results of more volatile games usually converge to the normal distribution much more slowly, therefore much more huge number of rounds are required for that.
Wizard Of Odds Poker Probabilities Odds
As the number of rounds increases, eventually, the expected loss will exceed the standard deviation, many times over. From the formula, we can see the standard deviation is proportional to the square root of the number of rounds played, while the expected loss is proportional to the number of rounds played. As the number of rounds increases, the expected loss increases at a much faster rate. This is why it is practically impossible for a gambler to win in the long term (if they don't have an edge). It is the high ratio of short-term standard deviation to expected loss that fools gamblers into thinking that they can win.
The volatility index (VI) is defined as the standard deviation for one round, betting one unit. Therefore, the VI for the even-money American Roulette bet is 18/38⋅20/38≈0.499{displaystyle {sqrt {18/38cdot 20/38}}approx 0.499}.
The variance v{displaystyle v} is defined as the square of the VI. Therefore, the variance of the even-money American Roulette bet is ca. 0.249, which is extremely low for a casino game. The variance for Blackjack is ca. 1.2, which is still low compared to the variances of electronic gaming machines (EGMs).
Additionally, the term of the volatility index based on some confidence intervals are used. Usually, it is based on the 90% confidence interval. The volatility index for the 90% confidence interval is ca. 1.645 times as the 'usual' volatility index that relates to the ca. 68.27% confidence interval.
It is important for a casino to know both the house edge and volatility index for all of their games. The house edge tells them what kind of profit they will make as percentage of turnover, and the volatility index tells them how much they need in the way of cash reserves. The mathematicians and computer programmers that do this kind of work are called gaming mathematicians and gaming analysts. Casinos do not have in-house expertise in this field, so they outsource their requirements to experts in the gaming analysis field.
See also[edit]
References[edit]
- ^'Roulette'. britannica.
- ^'D'Alembert roulette system'.
- ^'Online slots Return to Player (RTP) explained - GamblersFever'.
- ^'Return to Player and Hit frequency - What do these mean? - GetGamblingFacts'.
- ^https://www.okslot88.com/hal-yang-perlu-di-ketahui-tentang-mesin-slot-online/
Further reading[edit]
- The Mathematics of Gambling, by Edward Thorp, ISBN0-89746-019-7
- The Theory of Gambling and Statistical Logic, Revised Edition, by Richard Epstein, ISBN0-12-240761-X
- The Mathematics of Games and Gambling, Second Edition, by Edward Packel, ISBN0-88385-646-8
- Probability Guide to Gambling: The Mathematics of Dice, Slots, Roulette, Baccarat, Blackjack, Poker, Lottery and Sport Bets, by Catalin Barboianu, ISBN973-87520-3-5excerpts
- Luck, Logic, and White Lies: The Mathematics of Games, by Jörg Bewersdorff, ISBN1-56881-210-8introduction.
